UGDSB #1

Grade 9 Math + Coding Workshop

5 October 2021, (c) George Gadanidis

A. WHAT’S NEW?

GRADES 1-9

  • Coding across all grades, in algebra (and beyond).
  • Some more sophisticated mathematics.
  • A focus on the beauty, aesthetics and wonder of mathematics.
  • Social-emotional learning skills.

GRADE 9

  • De-streamed classes.
  • Research and tell a mathematics story.

B. BIG PICTURE #1

START WITH CODE THAT WORKS

  • Have students execute the code to see its output
  • Ask them to alter the code to model the different intervals in the table
  • Ask: how does the code do what the table does?
  • Ask them to share what they understand and what they have questions about
  • Have students try to answer one another’s questions
  • Don’t be in a hurry to explain

YOU DON’T HAVE TO BE THE EXPERT

  • Make “understanding” their “problem”
  • For example:
    • Print and post the code on a whiteboard
    • Draw arrows to the parts that students are unsure about
    • Students may use sticky notes to write/post descriptions of what the code sections do
  • The more you explain the less they will think about it

GET READY TO BE SURPRISED

  • I’ve spend many, many days in grades 1-10 classrooms co-teaching with math + coding
  • A common event is teachers telling me to look at a student whose engagement and understanding surprises them

C. INEQUALITIES

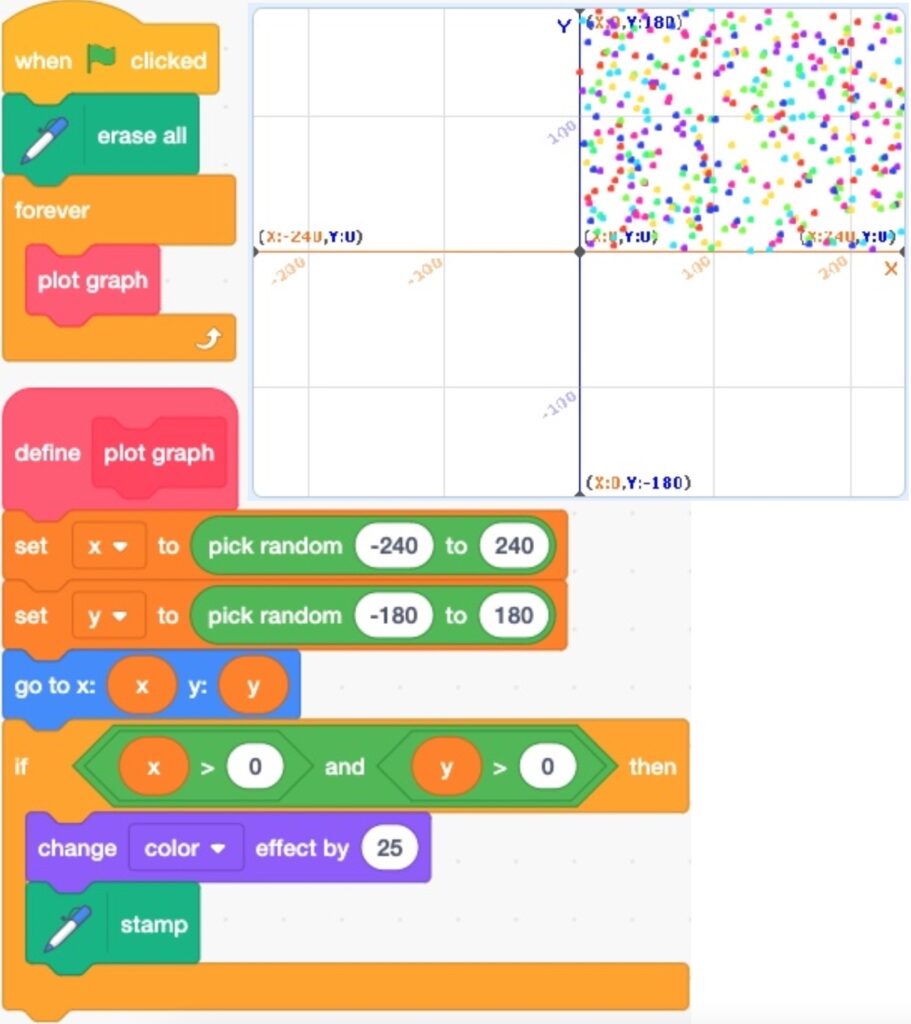
1. PUZZLE #1

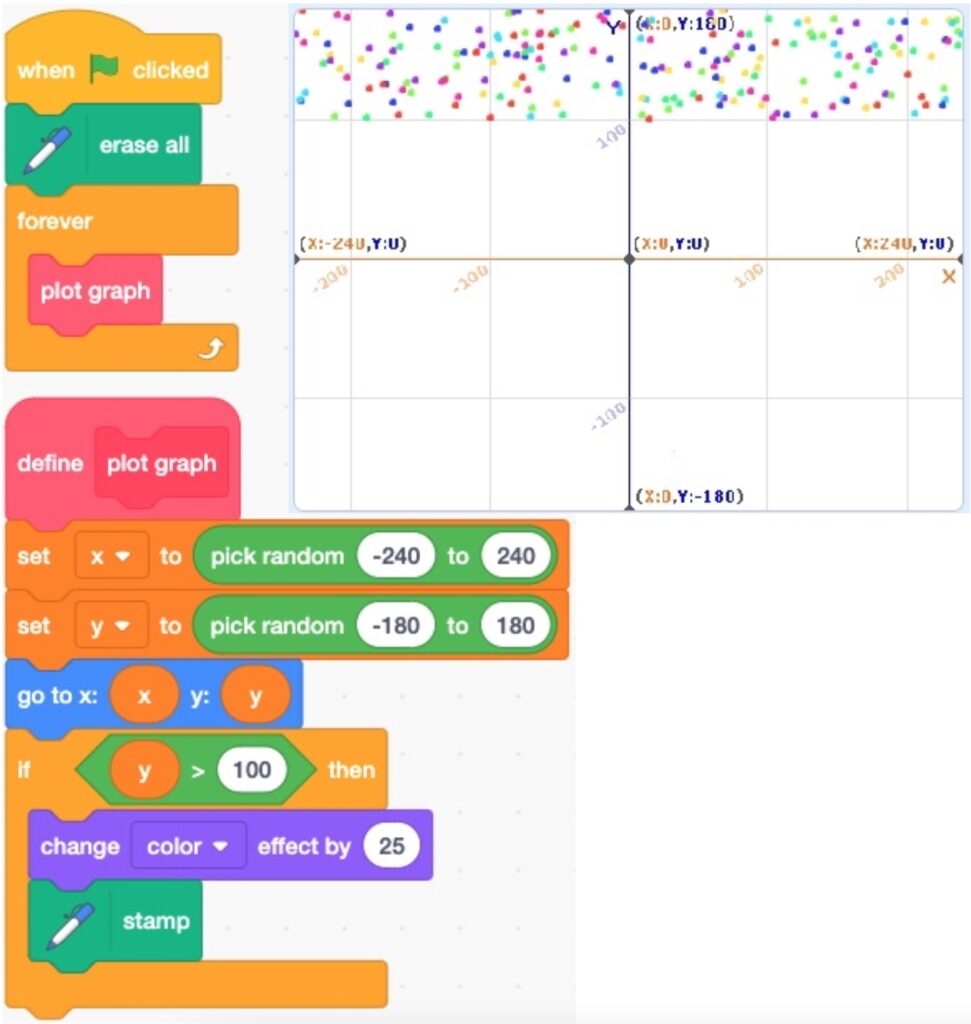
1.1

A. Alter the code to get the following output.

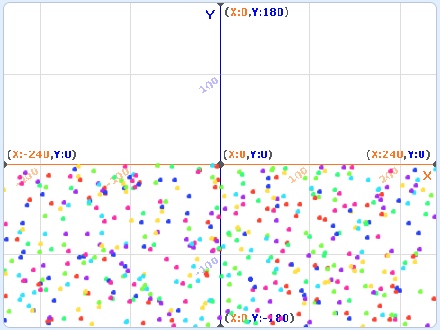
B. Alter the code to get the following output.

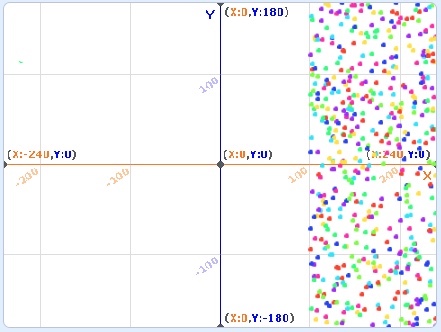
1.2

Alter the code in other ways and notice the effect.

  • What part of the code do you understand?
  • What part of the code do you have questions about?

2. PUZZLE #2

2.1

A. Alter the code as shown below.

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

B. Alter the code as shown below.

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

C. Alter the code to get the output shown below.

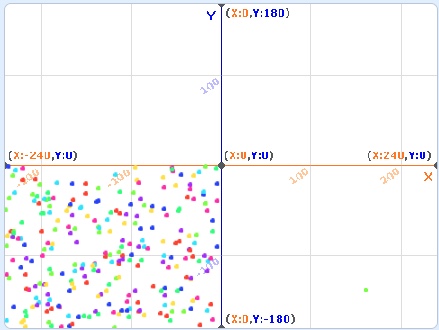
D. Alter the code as shown below. [Notice that “and” changed to “or”]

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

2.2

Alter the code in other ways to get similar results.

  • What have you learned about about inequalities and their graphs?
  • What else do you want to know?

3. PUZZLE #3 – grades 7/8

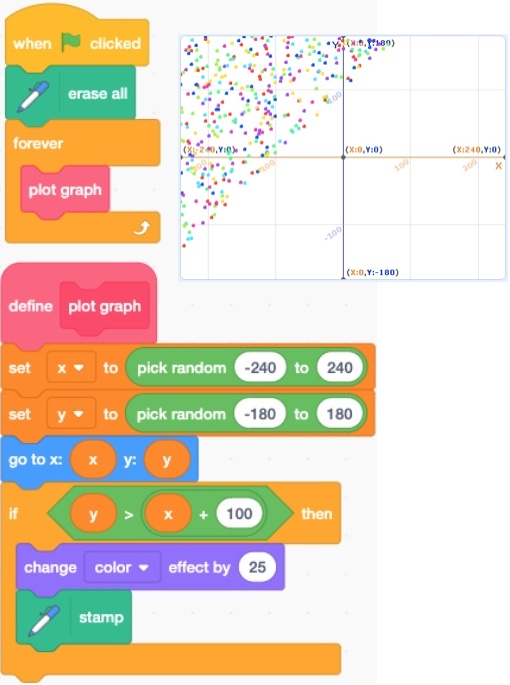
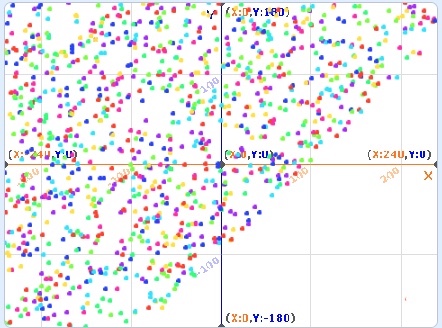
3.1

A. Alter the code to get the output shown below.

B. Alter the code to get the output shown below.

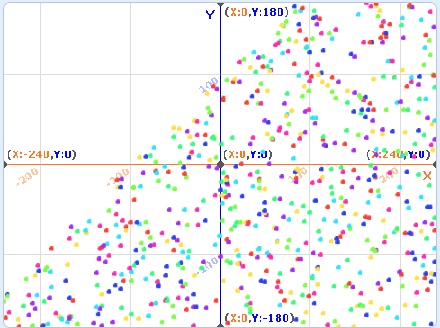
3.2

Alter the code in other ways and notice the effect.

  • What more have you learned about about inequalities and their graphs?
  • What else do you want to know?

4. PUZZLE #4 – grades 7/8

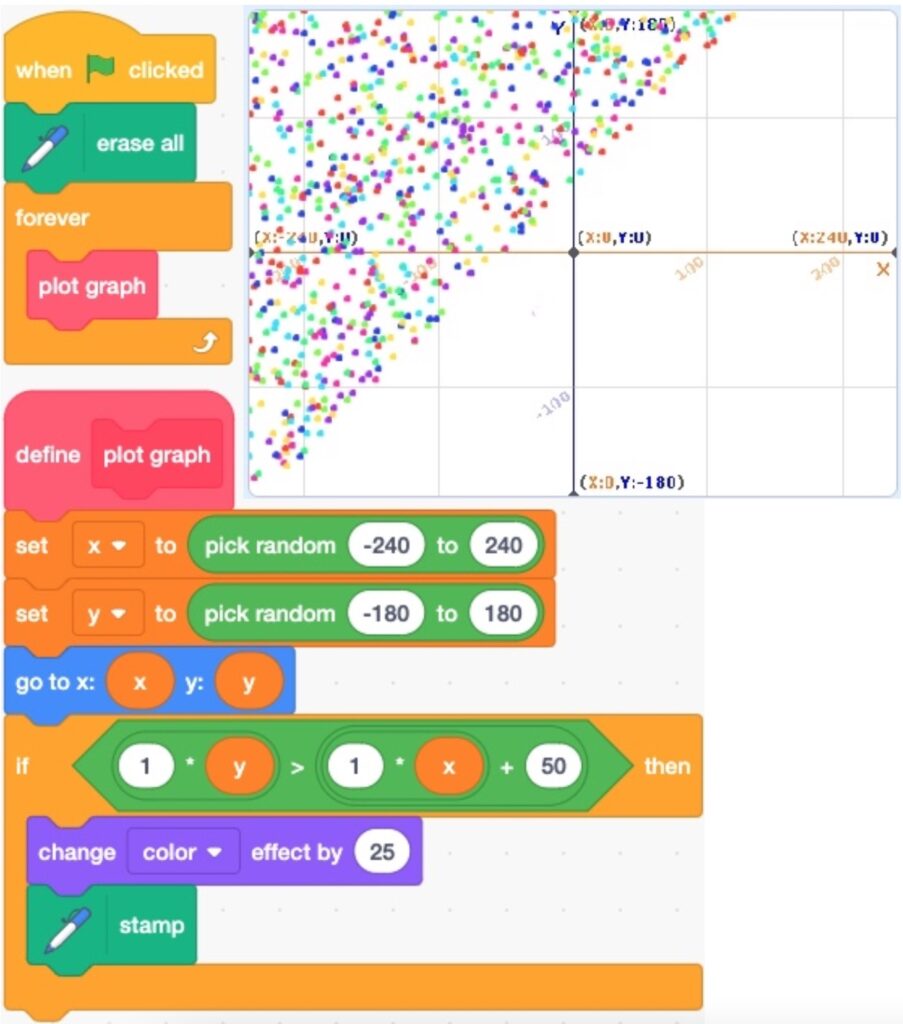
4.1

A. Alter the code as shown below.

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

B. Alter the code as shown below.

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

C. Alter the code as shown below.

  • Predict how the output will change.
  • Run the code to test your prediction.
  • Explain the result.

4.2

Alter the code in other ways to get similar results.

  • What more have you learned about inequalities and their graphs?
  • What else do you want to know?

Grades 5-6 WORKSHOP

See https://learnx.ca/w56s/

D. BIG PICTURE #2

CODING OFFERS ADVANTAGES

  • Coding models mathematics concepts & relationships dynamically
  • It makes abstract ideas feel tangible
  • It affords agency
  • It offers a low floor and a high ceiling
  • Coding has the potential to change what mathematics can be done and who can do it.

DON’T TEACH CODING, TEACH MATH

  • The pressure around us is to teach all kids how to code
  • Mathematics education is about offering all students access to the structure, beauty and wonder of mathematics
  • Coding is a great tool to think with, especially when we have good conceptual structure of the mathematics

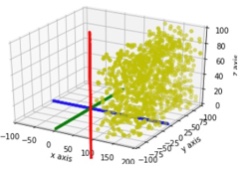
E. EVAPORATION RATES

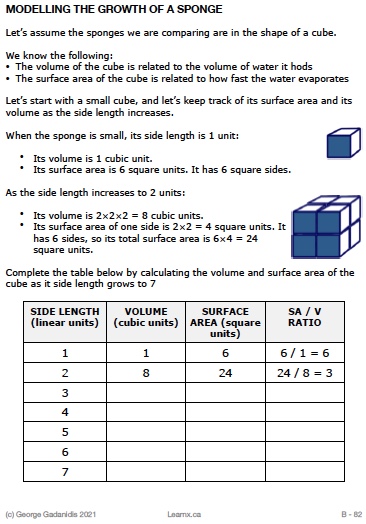
Let’s model this with Python –https://colab.research.google.com/drive/1I_AHVoWqFgWBZU7eEMMgBUK0pkJzlRPx?usp=sharing

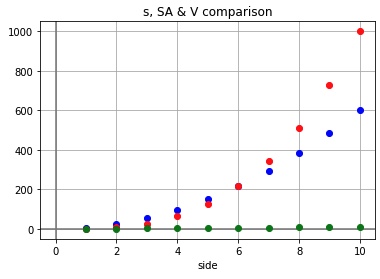
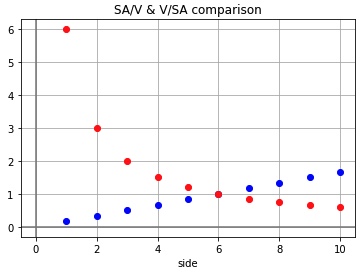
F. NATURAL DENSITY

Examples

  • d(even numbers) = 0.5
    • what is the probability that a random natural number is odd?
  • d(multiples of 5) = 0.2
    • what is the probability that a random natural number is a multiple of 5?
  • d(multiples 0f 10) = 0.1
    • what is the probability that a random natural number is a multiple of 10?

NATURAL DENSITY OF SQUARE NUMBERS

A SURPRISE

  • d(square numbers) = 0
    • what is the probability that a random natural number is a square number?

How do we make sense of d(square numbers) = 0 ?

Here is one way …

page 38

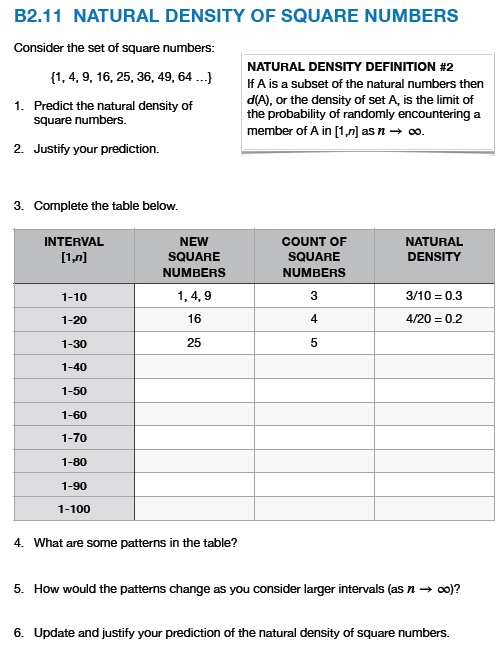
Here is the completed table.

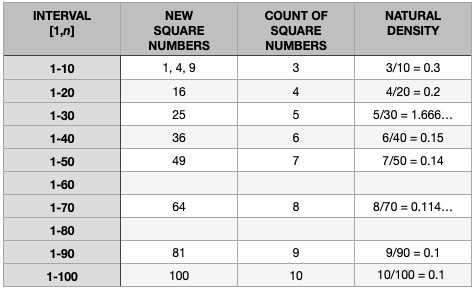
page 39

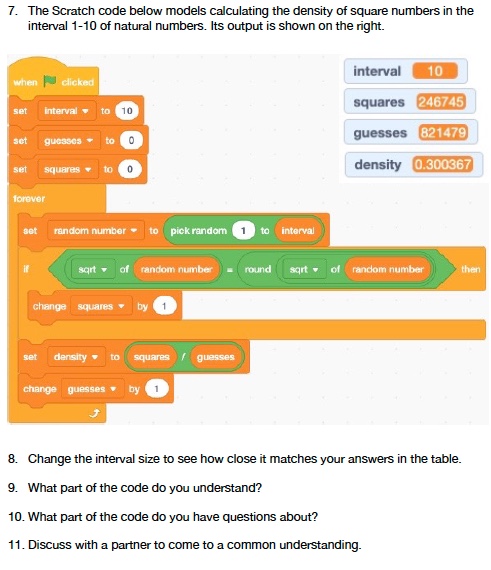
The Scratch code shown above is available at https://scratch.mit.edu/projects/565845359/editor

algebraically

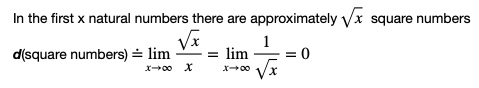
G. +/-/x RELATIONS

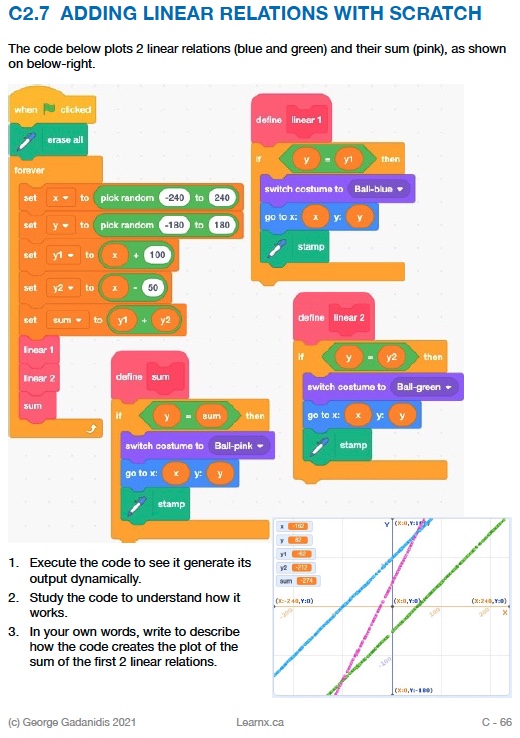
Adding relations … Try the code at https://scratch.mit.edu/projects/557365154/editor

Multiplying relations … Try the code at https://scratch.mit.edu/projects/557347523/editor/

H. READINGS

Integrated Mathematics + Computer Science – Grade 10: Reforming Secondary School Mathematics Education (April 2018). Read the White Paper by CT CoP members, George Gadanidis (Western University) and Jeff Cummings (Wellington Catholic DSB). See the Grades 1-3 lesson studies.

Coding in the Ontario Mathematics Curriculum, 1-8: Might it be transformational? Read the March 2021 report at http://mkn-rcm.ca/wp-content/uploads/2021/03/CL-mkn-v3.pdf