Lessons learned from research classrooms
by George Gadanidis, Western University
0. Introduction
Wonder is a feeling of surprise, combined with a sense of beauty or admiration.
Wonder makes us curious, attentive and eager to learn.

We have witnessed mathematical wonder in children in grades 1-2, as they noticed Odd numbers hide in squares! Then they wondered, Where do even numbers hide?
Below, based on many years of collaborating and co-teaching in research classrooms, I share what we have learned about helping students experience mathematical wonder.
- Wonder in mathematics
- Deeper mathematics
- A low floor and a high ceiling
- Good story, good math
- For all students
- Less is more
1. WONDER IN MATHEMATICS
Mathematics can be full of wonder!
However, the mathematics most of us have experienced in school lacked surprise and beauty, and it did not engage our curiosity.
PARALLEL LINES
For example, when we ask students and teachers what they know about parallel lines, they typically state that “parallel lines are straight and they never meet.”
Interestingly, about 2,300 years ago, the mathematician Euclid tried and could not to prove that parallel never meet. Neither could other mathematicians for the next 2,000 years. How could this be?
It turns out that “parallel lines never meet” is not a theorem to be proven. It is an assumption.
- If we assume parallel lines never meet, we live on a flat surface.
- If we assume they do meet, we live on a spherical or elliptical surface.
- Different assumptions lead to different geometries!
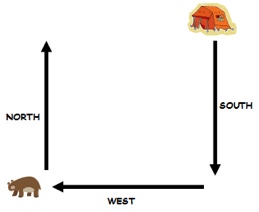
To see parallel lines meet, solve this riddle:
- Molly steps out of her tent.
- She walks south 1 km.
- She walks west 1 km.
- Sees a bear.
- She gets scared runs north 1 km, and somehow she finds herself back at her tent.
- How can this be?
- And what colour was the bear?
Here is how some prospective teachers reacted when learning that parallel lines are not as simple as “they never meet”:
I feel like I was misled, misguided, told the half-truth about parallel lines. It is the first time that I have realized and felt that math isn’t just BLACK & WHITE and can cause quite creative outcomes and discussions. (Gadanidis & Namukasa, 2007)
How is it possible that students come to believe parallel lines never meet, when they live on a sphere?
The geometry of parallel lines can be full of wonder.
Consider the spherical geometry of our world”
- Are lines of latitude parallel?
- Are lines of longitude parallel?
- What is a straight line on a sphere? Is it a line of latitude or a line of longitude?
- What’s a great circle and how many are there on a sphere?

- If a bug walks a balanced walk on a sphere, what would be its path?

- What paths do airplanes fly to travel the shortest distance possible?

- What is the sum of the angles of a triangle on a sphere?
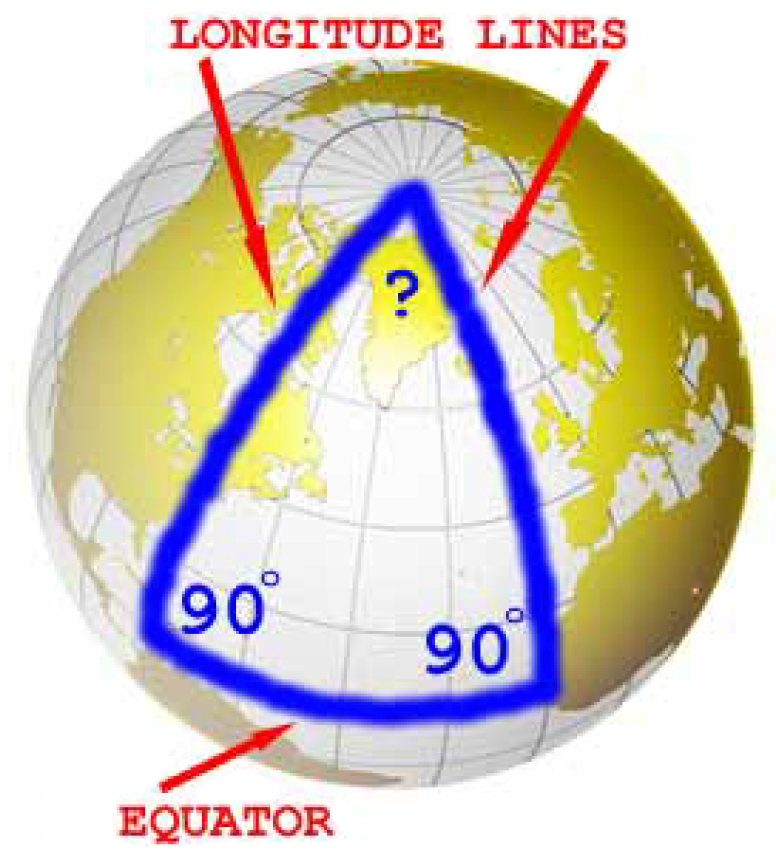
- What other geometries are possible?
WONDER & LEARNING
Wonder flexes our imagination, makes us curious and attentive, and motivates us to learn.
What mathematical wonders will students experience in your classroom?
_____________
- Gadanidis, G. & Namukasa, I. (2007). Mathematics-for-teachers (and students). Journal of Teaching and Learning, 5(1), 13-22.
2. DEEPER MATHEMATICS
Wonder becomes possible when we add depth to mathematics we bring to the classroom.
SHALLOW MATHEMATICS

Let’s consider this typical textbook problem:
A worker plans to install hardwood flooring in a room 3.2 m by 4.5 m. Each bundle of hardwood covers an area of 1.8 m2. He estimates a waste of 10%. How many bundles should he purchase?
This problem is solved using simple calculations. All measurements are constant. The mathematics is static and shallow.
To add mathematical depth, we may design a different problem, one that involves both area and volume, and investigate how these quantities change in relation to one another.
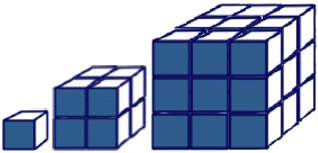
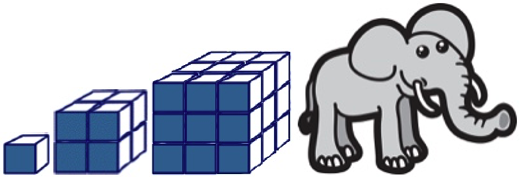
For example: How do surface area and volume change in relation to one another as a cube grows in size?
Investigating this relationship may also helps us understand why elephants have big ears.
WHY DO ELEPHANTS HAVE BIG EARS?

Why do elephants have big ears?
What do you think?
Model an elephant as a cube
Let’s measure the volume and surface area of elephants of various sizes and see what patterns emerge.
To keep calculations simple, let’s model an elephant as a cube.

A small elephant:
- The dimensions are 1 x 1 x 1.
- V = 1 cubic unit.
- SA = 6 square units.
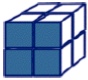
A bigger elephant:
- The dimensions are 2 x 2 x 2.
- V = 2 × 2 × 2 = 8 cubic units.
- SA = 6 × 4 = 24 square units.
An even bigger elephant:
- The dimensions are 3 × 3 × 3.
- V = 3 × 3 × 3 = 27 cubic units.
- SA = 6 × 3 × 3 = 54 square units.
Look for relationships
Let’s record measurements for the first 10 elephants in the table below.
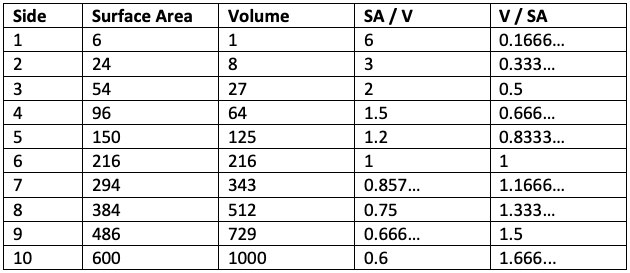
- What is the relationship between SA and V?
- Notice how SA/V and V/SA change.
- What is the meaning of each of these ratios?
What does this have to do with elephants and their ears?
Plot on a graph
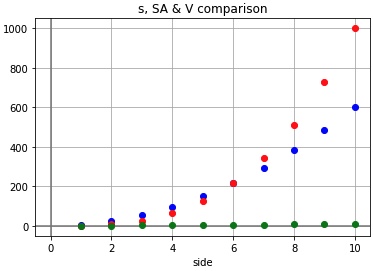
We may also display the data graphically.
Comparing SA and V
These scatter plots compare the growth patterns of side length, SA and V for cubes with side lengths 1-10.
- Which scatter plot represents SA? Green, red or blue? How can you tell?
Comparing SA/V and V/SA
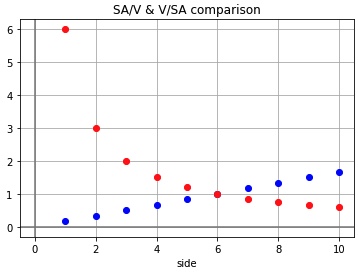
These scatter plots compare SA/V and V/SA.
- Which scatter plot represents SA/V? How can you tell?
- Why is the blue scatter plot a straight line of points?
Why do elephants have big ears?

Consider connections & extensions
We may also consider some related problems and extensions.
Which will evaporate first?
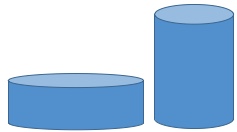
The containers have the same amount of water. Which will evaporate first? Why?
Which will dry first?

Both sponges are soaked with water. Which will dry first? Why?
Puppies in cars

Why is it unsafe to leave a puppy (or a young child) in a car on a hot summer day?
3. a low floor and a high ceiling
A low floor allows students to engage with minimum prerequisite knowledge.
A high ceiling offers students opportunities to investigate more complex concepts and relationships.
Here is one way we created a low floor and a high ceiling for the concepts of infinity and limit, which are typically studied in Calculus.
INFINITY & LIMIT
In grade 3, students usually learn area representations of fractions.
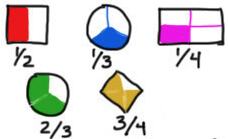
This creates a context for engaging students with infinity and limit.
HANDS-ON
Using squares of the same size, students shade to represent the fractions 1/2, 1/4, 1/8 and 1/16. This pattern can continue forever. It is infinite.
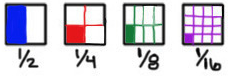
Using scissors, students cut out the shaded parts.

Imagine doing this forever, shading and cutting, and then joining the shaded parts to form a new shape. How big would the new shape be?

Students notice that all shaded parts fit in a single square.
A single square is the limit of the sum of this infinite set of fractions.
1/2 + 1/4 + 1/8 + 1/16 + … = 1
Students exclaim: I can hold infinity in my hand!
EXTENSIONS
We may also consider some related problems and extensions.
1. Infinity in pieces

Notice that some of the fraction pieces are square.
- What is the sum of the square fraction pieces?

Notice that the rest of the fraction pieces are rectangular.
- What is the sum of the rectangular fraction pieces?
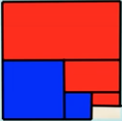
To answer these questions, it may help if you arrange the square and rectangular pieces like this.
2. Infinity in a walk
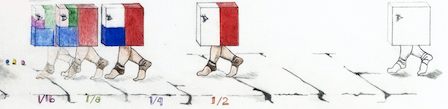
Imagine walking to a door this way:
- First you walk half way to the door.
- Then you walk half the remaining distance.
- Then you walk half the remaining distance.
- Then you walk half the remaining distance.
- You keep doing this forever.
Will you ever get to the door?
3. Infinity in a decimal
Consider the repeating decimal 0.999 …
Is 0.999 … equal to 1?
4. GOOD STORY, good math
One way to judge the quality of students’ mathematics experience is to consider how they would answer the question: What did you do in math today?
As you plan a mathematics activity, imagine how it may prepare students to answer this question.
Will students be able to share with family and friends an experience — a story — that would offer mathematical surprise and conceptual insight?



GOOD STORY, GOOD MATH

Brian Boyd (2009) says that story is a biological necessity.
Watson and Mason (2007) see mathematics as “an endless source of surprise.”
Creating, sharing and learning through stories and surprises are deeply human dispositions.
Interestingly, there is evidence that mathematics and storytelling are developmentally related.
Daniella O’Neill and colleagues (2004), from the University of Waterloo, tested young children’s narrative abilities. Two years later, they also tested their mathematical abilities.
Children with high-level narrative abilities, such as identifying stories with similar plots, or seeing a story from different character perspectives, also exhibited high-level mathematical abilities, such as pattern recognition.
STUDENTS AS MATHEMATICAL STORYTELLERS
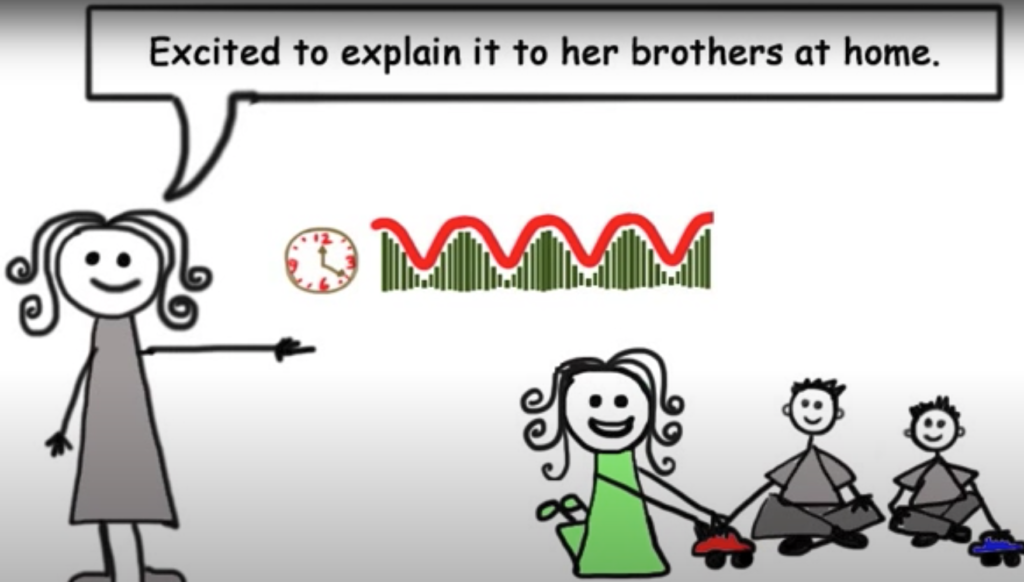
Here is one way we prepare students to share their learning at home.
- As students work on an activity, we record their comments, surprises and insights, and we share these with students as a handout. This gives students access to the collective knowledge of the class.
- We also provide students generic comic strip characters, along with images from their classroom work. Students cut and paste characters and comments to create comic strips that answer the question: What did you do in math today?
- Students share the comic strips at home. Parents report back: What did your child share with you? and What did you learn?
- We summarize parent comments and send them back to parents. Sometimes, we use the comments to create lyrics that students sing for their parents. Below is an example of such a song, based on grade 3 students creating bar graphs to represent and investigate circular relationships.
___________
- Boyd, B. (2009). On the Origin of Stories: Evolution, Cognition, and Fiction. Cambridge, MA: Belknap Press of Harvard University Press.
- O’Neill, D. K., Pearce, M. J., & Pick, J. L. (2004). Predictive relations between aspects of preschool children’s narratives and performance on the Peabody Individualized Achievement Test – Revised: Evidence of a relation between early narrative and later mathematical ability. First Language, 24, 149-183.
- Watson, A. & Mason, J. (2007) Surprise and inspiration. Mathematics
5. FOR All students
Our schools are democratic institutions. They provide access to education for all students.

However, as educators, we sometimes worry that deeper mathematics may confuse students.
We also worry that students who typically struggle mathematically may not be ready.
This occasional lack of faith in children’s abilities is, in part, due to some popular, but incorrect, education theories.

Jean Piaget, for example, brought to us the theory of stages of cognitive development. He said that young children are concrete thinkers, and they develop their capacity to abstract later, maybe around age 12.

Seymour Papert, who worked with Jean Piaget, disagreed. He said the stages Piaget identified are not in children’s minds. Rather, these stages are symptoms of how we educate children.
Piaget (1972/2008) himself cautioned about how generally his stages of development may apply.
Fernandez-Armesto (1997) lamented that “Generations of school children, deprived of challenging tasks because Piaget said they were incapable of them, bear the evidence of his impact” (p. 18).

Kieran Egan (2002) noted that young children naturally abstract to develop language, and come to understand words, such as dog.
Dogs are big, small, different colours, and with different dispositions. Children create an abstraction of the essential characteristics of dogs, and distinguish them from other animals that look like them.

Children effortlessly abstract at a young age. They are much more capable, and much more attracted to deep ideas of mathematics, than we sometimes assume.
As one teacher noted:

I found that sometimes the tasks we might feel initially [to be] difficult, the kids got just like that. It has made me less fearful to go beyond the curriculum. In Grade 4 you’re only supposed to learn this. Well, what’s stopping us from showing them a little bit beyond that?
Another teacher said:
I wish you were here to see the kids that never do well on assessments. I’ve never seen that part of him. Words coming out were impressive.
A low floor and a high ceiling approach is one way to offer access to deep ideas of mathematics for all students.
_______________
- Egan, K. (2002). Getting it wrong from the beginning : our progressivist inheritance from Herbert Spencer, John Dewey, and Jean Piaget. New Haven :Yale University Press.
- Fernandez-Armesto, F. (1997). Truth: A history and a guide for the perplexed. London: Bantam.
- Papert, S. (1980). Mindstorms—Children, Computers and Powerful Ideas. New York: Basic Books, Inc.
- Piaget, J. (2008). Intellectual evolution from adolescence to adulthood. Human Development, 51, 40-47. (Original work published 1972)
6: Less IS more
Implementing a few mathematics activities that offer wonder, and doing this well, is the ideal way to get started.
Start small.
Focus on deeper mathematics.
Engage students in sharing their learning beyond the classroom.

A few well-designed mathematics experiences can have lasting impact on students’ and teachers’ dispositions, living fruitfully in future experiences — as Dewey (1938) has suggested — by raising expectation and anticipation of what mathematics is and what it can offer (Gadanidis, Borba, Hughes & Lacerda, 2016).
What wonderful mathematics stories — what mathematical surprises and conceptual insights — might you help your students experience?




____________
- Dewey, John (1938). Experience & Education. New York, NY: Kappa Delta Pi.
- Gadanidis, G., Borba, M., Hughes, J. and Lacerda, H. (2016). Designing aesthetic experiences for young mathematicians: A model for mathematics education reform. International Journal for Research in Mathematics Education 6(2), 225-244.