MATH INTERVIEWS

The interviews below by George Gadanidis were originally published in 1999-2001 in the magazine Math Mania – Adventures in Mathematics.

Gilbert Labelle

Gilbert Labelle is Professor of Mathematics at the Université du Québec à Montréal. He was born in 1944 (June 8) in the town of Longueuil, south of Montréal. His 3 brothers, Denis, Jacques, and André are also mathematicians. Their parents, Lucien and Yvette, were artists.

Gilbert, what do you like about math?

I like mathematics because it is beautiful, full of surprises, gives me complete freedom of thought and, at the same time, it can be applied efficiently to solve problems in science and society.

When you were young, did you like math the best?

In fact, when I was very young, I liked every subject, from art to sciences.

How are art and mathematics similar or different?

They are similar in that they both use human imagination and skill to combine things to create new things. However, in mathematics, everybody agrees in the way things are combined while, in art, things are combined according to individual feelings. Of course, this does not prevent mathematicians from having individual feelings and artists from having universal conventions.

What does a mathematician do?

Essentially, a mathematician uses his or her imagination to combine ideas, as clearly as possible (using formulas, geometrical figures, computers, etc), to create new ideas and to provide a language and a way of thinking for all Science.

What is your area of research?

My area of research in mathematics is Combinatorial Analysis. It is essentially a subject of pure mathematics, but it is closely related to applied mathematics and Computer Science.

How is Combinatorial Analysis used?

Combinatorial Analysis is useful in organizing and compressing data structures in Computer Science; in defining symmetries of molecules in Chemistry; in analysis of DNA and the classification of species in Biology; and, in many other human activities, like encoding compact discs, encrypting transactions, and designing flight schedules.

Can you give us a simple problem that involves Combinatorial Analysis?

Suppose you tossed a coin twice. What are the possible outcomes? In answering this question, you could use Combinatorial Analysis.

If I tossed a coin twice, I could get two heads, two tails, or a head and a tail.

True. Which of these combinations do you think is more likely to occur?

Hmm. I think the one head and one tail combination is more likely to occur. Is this correct?

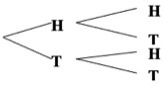
You could use a tree diagram to help you decide.

I see. There are four possible outcomes: HH, HT, TH, and TT. And two of the outcomes involve a head and a tail.

A diagram like this, which helps represent the various combinations, is called a combinatorial structure. A combinatorial structure can often be thought of as a “skeleton” of a more complicated object (from the real world or from the world of ideas).

Can you give us some other examples of combinatorial structures?

A map connecting towns through roads is a combinatorial structure, which schematically represents real routes connected by real roads. Another example is the output of a computer program (or even the computer program itself!).

Something to Think About

What does Gilbert like about math?
What do you like about math?
What does a mathematician do?
What is a combinatorial structure?

Nathalie Sinclair

Nathalie Sinclair was born in France but grew up mostly in Calgary, Alberta. She is a professor at Michigan State University. She has also travelled a lot, living for two years in France, Italy and Greece.

Why do you like math, Nathalie?

I like mathematics because it so often shows how one small change, like transforming an equation, introducing a new dimension, or seeing a different representation can give you a whole new feeling of how something works and how it connects to other things that we do or think about. I like the feeling of understanding something, seeing new connections, and of being able to admire the creativity of other mathematicians.

Why do you think some people don’t like math or are afraid of math?

I have found that most children love to do mathematics but that as they move through school mathematics goes further and further away from the things they know and enjoy. As they start experiencing disinterest and continued failure, they become afraid of the subject.

What do you enjoy the most when working with students doing mathematics?

I love how excited the students can get about mathematics, how many of the topics can transform the way they think about or see things. I love learning about how they look at mathematical situations and seeing what sparks their interest.

What kind of mathematics do children enjoy most?

The students that I have worked with really enjoy geometry, whether it’s figuring out how to get around on a grid, transforming shapes or visualising operations on three-dimensional objects. This is an area in which they have a lot of intuitive knowledge from everyday experience, that they find appealing and in which there are lots of interesting problems to explore.

Why did you decide to do a doctorate in mathematics education, Nathalie?

I began teaching at a middle school after I had finished my Master’s degree in mathematics. At the same time, I was working at Simon Fraser University, developing educational technologies for mathematics learning which I was able to try out with my students. I became so interested in this that I decided to do a doctorate in mathematics education.

What is your research focus in your doctorate?

I have two main focuses in my work. The first is on the role of aesthetics in mathematics learning. The second is on the development and design of computer-based technologies. The two have some interesting meeting points!

What do you mean by aesthetics, Nathalie?

Aesthetics is partly about discerning patterns or perceiving relations and taking note of how things relate to one another and how they seem to fit together. When we experience things fitting together, they often look beautiful to us, and they often bring us a sense of pleasure.

How is math beautiful? Can you give an example?

I think that mathematics can be beautiful to different people in different ways. Some students love how fractal geometry transforms the way they see trees and clouds. Other students love the feeling of fitting different shapes together to create tessellations. And other students find it beautiful how you change a long and ugly equation into an easy one, always keeping it balanced, by repeatedly simplifying it. Often mathematics is beautiful when it lets you see something in a new way or remind you of something else that you already know or enjoy.

Something to Think About

Why does Nathalie like math?
What kind of math do you enjoy the most? Why?
How does Nathalie think that math beautiful?

Karen Amanda Yeats

Karen Amanda Yeats is from Halifax, Nova Scotia. She is math student at the University of Waterloo, in Ontario. In her first year she won the Special K (a competition UW sets up for its frosh). The year before that she did very well on the Descartes contest and quite well on a lot of other things (she received a scholarship for that).

Karen, what do you like most about math?

I like math because it’s beautiful, and because working with it is fun. I considered going into music composition, and I really feel the aesthetics of the two subjects are very closely related. The search for elegance.

What do you mean by elegance, Karen?

Elegance is a particular type of beauty, the type that comes from something very simple giving rise to something very complex or profound. In the same way that often you know when you’ve done a good job performing a piece of music when you made it seem effortless.

What’s it like to study math at the university level?

I’m really enjoying it. We do a lot more theoretical stuff than I did in high school or junior high. For me the theoretical stuff is far more interesting than calculations and applications. The assignment questions actually necessitate thought rather than just application of what was learned. Because of the focus on proofs the level of rigour required is much higher than before as well.

What is rigour, Karen?

Proving something rigorously is proving it so that not only do you believe it and not only can you convince other people by your argument, but you can show that no one can possibly ever find that you were wrong. It is very satisfying to be able to show without a shadow of a doubt that something is mathematically true.

What other interests do you have besides math?

Music, as already mentioned, is a major interest of mine. I play clarinet and recorder; I sing in choirs and I compose when I have the time. I’m currently in two orchestras, a baroque trio, a chamber choir and I take private lessons on recorder. I really enjoy these things They take up a lot of my time but really, I wouldn’t be happy without them.

What advice would you have for students who want to excel in math?

Read things on the subject. Write lots of math contests, because they’re fun and the more you write the better you do. Find someone to coach you, there are lots of teachers who would love to have a student who truly loves math rather than just needs it to graduate or do something with. Most importantly, never stop enjoying it. In fact, whatever you want to excel in make sure it is something that at times just leaves you with a feeling of wonder at the marvellousness of the universe.

Anything else, Karen?

Don’t ever feel that you need to justify math by its usefulness. Yes, it is useful, in many, many ways, but I don’t value it for its use. Its value is in its elegance. In this way I feel math is more of an art than anything else. So many people ask what use theoretical math can have, what good is it, what is it for? For me the answer to those questions could all be negative, and math would still be worth doing. Music has no practical justification, nor do the other fine arts, math doesn’t need one either.

Something to Think About

Why does Karen like math?
What do you like about math?
How is math like music?
What does Karen mean by rigour?
What can you do to become better at doing math?

Walter Whiteley

Walter Whiteley is professor of mathematics at York University, in Toronto. His work as a mathematician is in the field of geometry.

Walter, what is geometry?

Like all of mathematics, geometry is the study of patterns. The patterns of geometry are found in space and in the plane. The search for patterns and the pleasure, the surprise and the excitement of ‘seeing’ the same pattern in many places is my experience of mathematics. As you can see, to me mathematics is very visual. Of course, patterns are not just fixed images. They are dynamic: changing and evolving. Geometry is the study of these transformations – of how patterns shift under reflection, rotation, projection, and so forth. We look at the changing appearance of something – but then really focus on what did not change.

What kind of work do you do as a mathematician?

My work in mathematics is really playing with patterns and searching for patterns. I apply the patterns of geometry outside of mathematics. I compare the patterns in problems like: how to program computers to describe, change and manufacture shapes like the hood of a car; how a robot can find 3-D shapes from one or two camera pictures; what shapes of buildings stand up or fall over; whether a robot arm can reach an object; how parts of a protein move and how a drug changes the movement. In all of these I find common patterns – patterns I can literally ‘see’, after lots of practice.

How do you go about finding patterns, Walter?

I spend a lot of time learning about the basic pattern, working with a structural engineer and geometer. Patterns about some points and distances, or rigid bars and flexible joints and when the framework is stiff or shaky. Then I find the same pattern in a second place. After that, it was easier to find it in a third and a fourth place. I explore these patterns with models, in the computer, on paper and in my mind’s eye. I have several ways to represent the pattern – and I switch among them looking for connections.

Have these patterns been studied by other mathematicians?

These are patterns people have studied for a long time. James Clerk Maxell, known for his laws of electricity and magnetism, studied these patterns. We ask some new questions about the old patterns because we need to tell computers how to do the geometry. Some questions are new because we now ‘see’ proteins for the first time. The shape and motions of a protein can make the difference between health and disease. The same patterns are in something that small, as well as in things as large as a network of satellites.

Do you work mostly with diagrams?

I use diagrams the most – but these are diagrams with labels, and connections – really a mix of visuals and symbols. I love programs like Geometer’s Sketchpad because these moving images are really important in my thinking. Sometimes the computer sketch shows and expands what I was already doing with images in my own mind. Sometimes it puts the visual pieces into a larger pattern I had never seen before. It takes lots of practice to ‘see’ which parts of an image are important and which are distracting details. I would say we spend our whole lifetime learning to see.

Do you use hands-on materials?

Another way that I learn to picture a problem is to play with physical models and examples. This is often how I start a new problem. Building a model puts images and patterns into my brain. It helps me think carefully about some of the parts of the pattern. If you don’t know what you want to build, to model, you realize you don’t understand the problem yet. These tools are great to play with – but that play is something that you keep doing as long as you do mathematics. One reason people don’t see mathematicians playing like this is that we have learned to play in our minds.

Walter, do you ever use symbols as we do in algebra?

At stages of a problem in geometry, I do a bunch of algebra, working with equations and calculations. However, when these calculations are finished, I work hard to create visual patterns in which I can see these results. It is the images that I remember, the images which I play with and manipulate to see even the algebra more clearly. It is really important to do everything several different ways. I actually ‘do algebra’ visually. Everything is based on visible patterns. What do I see – and what does that suggest I should try next? Lots of algebra is what I call ‘cosmetics’. Changing what something looks like without changing what is really there underneath. What it ‘looks like’ suggests what I should do next in algebra. Sometimes, when I am stuck, I try changing the appearance in several ways, so that I might ‘see’ what to do as the next step.

How long do you work on a problem?

Working on a problem may not take just a day or a week. I have worked on some problems for years and then solved them. I think about some problems people have been working on for centuries. I feel connected to the other people who also thought about the problem in the past.

How do solutions to problems come to you?

Sometimes, mathematicians talk about ‘intuition’ but they are talking about how they play with images, see how the pieces fit together and see the solution – all without any words – but with lots of hard work. People do solve math problems in their dreams. I have. When that happens, it is a picture that I remember, and the picture is then put into symbols and words as one step towards being sure and convincing other people.

Does every mathematician solve problems the same way?

As researchers take pictures of our brains doing mathematics, we realize that different parts of mathematics are done in different parts of the brain. Different people do the ‘same mathematics’ very differently. This is important. A student and a teacher may not do something in mathematics the same way. Students who could do well with problems in visual form but are not so interested and so practiced in algebra may get discouraged. This should not happen. Many people in mathematics, do their best work visually. However, you may have to struggle through several years of ‘algebra’ in late high school and even the first years of university before things open up again and you realize that mathematics is so much more. Too often what people put in the books is not what they really do. Instead, it is what they have found people want to hear.

What gives you most pleasure when working with mathematics?

What gives me the most pleasure is when, after a long time working on a problem, getting parts of an answer, it all comes together in a single, powerful picture. I ‘see it’ as a whole and can find all the connections just by turning this image around in my mind. In mathematics we talk about ‘Theorems’. This word comes from the same root as Theatre. A theorem is something you have played with enough to say, ‘I see!’.

Walter, do mathematicians work alone?

I don’t want to do mathematics alone. Unless someone else is also interested in the problem, or I can tell them a good story and capture their interest, I will lose interest myself. I enjoy doing mathematics with a group of people interested in the same problem. If we have different approaches, that is good. When, together, we see the answer it is even more fun than doing it alone.

Something to Think About

Why is geometry?
How does Walter work to study and understand geometric patterns?
What does Walter enjoy when working on math problems?

Carolyn Kieran

Carolyn Kieran is a Professor of Mathematics Education in the Mathematics Department of the Université du Québec à Montréal. She trains future teachers of secondary school mathematics, drawing on her own experience as a secondary school math teacher in Montreal during the 1960s and 70s.

How did you get involved with math, Carolyn?

As far back as I can remember, I always loved mathematics and mathematical puzzles. It was my favourite subject in school. So, it seemed quite natural for me to become a teacher of high school mathematics. I found that I liked teaching mathematics as much as I liked doing mathematics itself. Seeing students turn on to mathematically challenging tasks proved very rewarding to me. After taking a leave for a few years to attend to my family, I returned to mathematics, but this time as a teacher trainer.

What is the focus of your work in math?

The bulk of my research in the teaching and learning of mathematics has been in the area of school algebra. Then when computers became available in schools, I decided to see how computing technology–and this includes graphing calculators–could be used to make algebra learning more meaningful.

What is algebra?

To me, algebra has three main parts. One part deals with creating and making sense of algebraic expressions and equations; another part with manipulating those symbolic objects; and the third part with activities like proving, generalizing, and problem solving that are not exclusive to algebra–they could in fact be engaged in without using any algebra at all–but which give context and meaning to school algebra.

Is school algebra changing?

Yes, school algebra is changing. It used to focus almost exclusively on symbol manipulation, with students being taught principally the rules for transforming expressions and solving equations. But the arrival of computers and graphing calculators did two things to change the face of school algebra. First, they made it easier to generate graphical representations, which opened up the “meaning” dimension of algebraic expressions. Second, the development of Computer Algebra Systems (CAS) raised questions about the amount of by-hand symbol manipulation students needed to engage in. School algebra is now in a kind of transition phase while educators try to sort out how best to blend the old with the new.

What does it mean to think algebraically?

To think algebraically is to see the general in the particular, to reason about relations rather than the specific quantities that are being operated with, to notice that which is varying and that which is constant in transformations, and so on. However, thinking is not simply communicating with oneself; it is an inherent part of communicating with others. Thus, thinking algebraically naturally entails speaking and writing algebraically, that is, using algebraic symbols according to the conventions and rules agreed upon by the mathematical community.

Carolyn, can you give an example of an algebra problem that you find interesting?

There are several reasons why I like the following problem that I have used in my research: It is open-ended, accessible to students of different ages, can be done without algebra, and lends itself to interesting approaches when a graphing calculator is available–although this tool is not necessary for its exploration. It is called the Growing Rectangles problem.

Growing Rectangles

Each of the following three families of rectangles has its growth pattern:

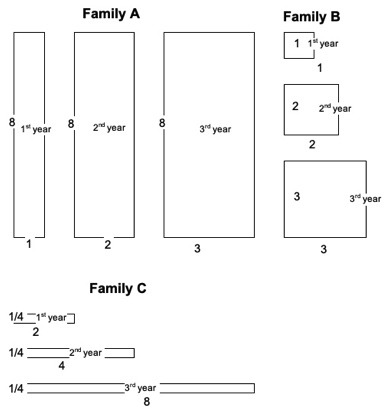
In family A the width grows each year by one unit; the length remains constant at 8 units. In B the width and the length of the rectangle grow each year by one unit. In C the length doubles each year, and the width remains equal to 1/4.

Please investigate the problem in groups. At first try to generate various hypotheses concerning the following questions:

1. Please compare the areas of the 3 families of rectangles over the years. What are their initial situations? Which family (or families) takes over the other families (or family) and when?

2. In which years will the area of each family exceed 1000 square units?

Please write a report as a common product of your group.

Try to describe your conjectures and what they were based on. What kinds of debates did your group have?

Try to describe the ways in which you solved the problem.

Chris Essex

Chris Essex is a professor in the Applied Mathematics Department of the University of Western Ontario, Canada.

What do you like about mathematics, Chris?

Mathematics is the purest form of clear thinking. Clear thinking of that type is one of the things that make humans special. Some creatures are fast, some are strong with big teeth, but it’s people who are the winners when it comes to thinking.

What does a mathematician do?

My job as a mathematician is to look after the mathematical knowledge that has accumulated over the centuries, and maybe add a bit to it and pass it on to you and your children. I am thrilled and honoured to be part of this great human undertaking across generations.

How is technology changing how and what mathematics is done?

It is important to realise that technology has always been around in mathematics. Mechanical computing machines are many generations old too. What is new today is that computing power is becoming cheap and convenient to use. This has caused people to do mathematics that they would not otherwise be able to do and see things they would not otherwise be able to see. But it really is not creating any kind of global change in the truth of the mathematics itself. This is not really so surprising as computers cannot really do mathematics. They imitate it, but only people do it.

How do computers ‘think’ mathematically differently from humans, Chris?

No computers, which people use for mathematics today, think. Thinking is what humans do. You need to remember that computers are limited tools. They are useful, but they cannot replace the “computer” between your ears.

Can you give us an example of mathematics that is done best using a computer?

Mathematics is an imprecise word for a subject that prides itself on precision in language. What does it mean to “do” mathematics? If it means to prove theorems, then computers are not very useful, although there are some notable exceptions, such as the map colouring problem. If it means instead to use mathematical results to understand the world, then computers tend to show up as useful in nearly every case. Nearly everything that is understood about our world can be and is expressed in mathematics, and computers are the key. From forecasting the weather, to doing special effects in the movies; mathematical techniques with computers are a significant part of our lives.

Are computers and calculators ever wrong?

Many people believe that computers are “smarter” than they really are. This is even true for people coming to universities. An important part then of mathematical training is to show people where computers go wrong.

Can you give us an example, Chris?

Try completing the table below using a calculator or a computer program. You may be surprised at the result.

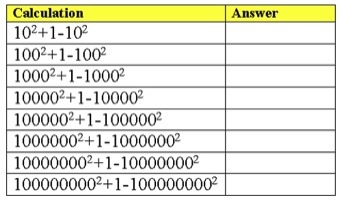
Something to Think About

Why does Chris Essex like mathematics?
How are computers useful in mathematics?
Can a computer or calculator think? Explain.
Explain the results in the table above.

Ved Madan

Dr. Ved Madan is a professor in mathematics and computer science at St. Mary’s College in Calgary, Alberta, Canada. He is currently teaching Mathematics Appreciation, Calculus, and Introduction to Computers courses.

What is your favourite math problem, Ved?

One I have always really liked is the area problem posed in 1917 by the Japanese mathematician Kakeya and solved in 1928 by the Russian mathematician Bescovitch: What is the smallest area inside which a line segment of unit length may be turned through 360⁰?

Can you explain this problem?

Imagine holding a piece of chalk flat against the base of the blackboard and turning it end-over-end twice, without raising the chalk off the blackboard. The chalk will trace two overlapping half-circles, whose radii are the length of the chalk.

You could also turn the chalk 360^o about its centre. The chalk will trace the area of a circle, whose diameter is the length of the chalk. This area would be smaller.

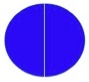
This is true. Can you see another way of moving the chalk so that it ends up turning 360^o, and the area it traces out is less than the area of the circle?

Is there another way?

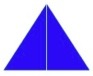
Suppose you draw an equilateral triangle; whose height is equal to the length of the chalk. You move the chalk inside the triangle so that it turns 360^o. The area traced by the chalk would be less than 75% of the area traced when you could turn the chalk 360^o about its centre.

That’s interesting. Touching one vertex, you turn the chalk from one side to the other, then you slide it to the next vertex and turn again, and so on. You could also use a square, turning the chalk from side to side, but I think the area would be bigger.

If you use a hypocycloid, an equilateral triangle whose sides are the same length as the chalk but are bent inwards, the area traced by the chalk would be less than 50% of the area traced when you could turn the chalk 360^o about its centre.

What other figures could you use?

You could turn the chalk 360^o by moving it inside a five-point star, as shown in the diagram. The area traced by the chalk would be less than 40% of the area traced when you could turn the chalk 360^o about its centre.

What happens as you add more points to the star?

As we increase the number of points of the star, the area traced by the chalk approaches zero.

It is amazing that you can turn the chalk 360^o in an area that is almost zero.

It certainly is.

Something to Think About

Demonstrate to another student how the chalk moves to create each of the shapes described in the interview with Ved Madan.
Do you agree with Ved Madan that as we increase the number of points of the star, the area traced by the chalk approaches zero? Explain your thinking.

Larry Davidson

Larry Davidson works for the Engineering Department of the City of London, in Ontario, Canada

Larry, what type of work do you do?

Lately I’ve been doing a lot of surveying. I help create three-dimensional drawings of the streets in London, showing the distances between driveways, widths of roads, thickness of roads, where the maintenance holes are, etc.

How do you make the drawings three-dimensional?

It’s quite neat actually. We take the measurements and enter them into a computer program that creates the three-dimensional image. You can rotate the image and see a street from different angles and different elevations.

How do you take measurements?

We use an instrument known as a total station that is a combination of a transit and electronic distance-measuring device.

A transit measures angles. Is that right?

Yes, it does. The transit we use is very sophisticated. It has an auto-tracking feature that uses a radio signal to automatically keep track of changing angles.

When you are out taking measurements, how do you know where you are exactly on the city map?

There are marker plaques around the city of London that show the exact longitude, latitude and elevation. These coordinates were taken using satellite imaging and they are very accurate. We set up our device over one marker and orient it towards a second marker. This becomes our baseline for any measurements we make. The computer software uses this baseline to integrate our measurements into the rest of the city map.

Why are you creating these maps?

We’re mostly concentrating on the older streets that may need some work in the near future. These maps will help us identify what needs to be done and how much it may cost.

What would we see in the three-dimensional maps if we looked under a street?

You would see sanitary sewer pipes, storm sewer pipes, and freshwater pipes.

What do the sanitary sewer pipes do?

In a city, all the stuff that goes down a drain or a toilet in your house ends up in the sanitary sewer, which carries it to a treatment plant. There the water is cleaned and then released into a nearby river or lake.

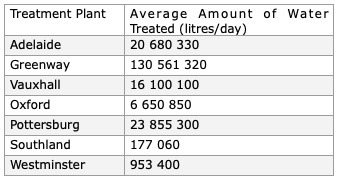
How much water is treated at these plants?

There are seven different treatment plants in London. The average daily amount of water treated at each plant varies.

How big are the sanitary sewer pipes?

They vary in size. Eight inches, or 200 mm, is a pretty common diameter.

How do you know how big to make the pipes?

It all depends on how many people the sewers serve. Theoretically, each person uses about 400 litres of water per day, through showering, using sinks and toilets, washing clothes, etc.

Do the sizes of storm sewer pipes also depend on the number of people using them?

Actually, no. Storm sewers are not typically connected to drains from houses. Their job is to carry water from rain and melting snow to the nearest creek or river. The size of storm sewers depends on the size of the drainage area and on the type of drainage area.

How do different types of drainage areas affect storm sewers?

Well, if the drainage area is mostly parkland, with lots of grassy areas to absorb water, then the storm sewer pipes would not need to be as big as in an area that is covered with roads and buildings, where most of the rainwater runs off into the storm sewers.

What happens if a park area is developed into houses?

Then you either make the storm sewer pipes bigger or you create a holding area for the water to control how fast it gets to the storm sewer pipes. Otherwise, you can end up with flooding problems.

What do you like most about your job, Larry?

I like the fact that I get to work on many different projects around the city. I also like working outdoors.

Thank you for this interview, Larry.

You’re very welcome.

Something to Think About

Find the latitude and longitude coordinates of your school. You’ll have to do some research in your library or on the internet.
How is the latitude and longitude coordinate system similar to the x-y coordinate system? How is it different?
Do you think lines of longitude are parallel? Explain your reasoning.
Do you think lines of latitude are parallel? Explain your reasoning.
Consider the table on the previous page.
1. Find the average amount of water that is treated in London per day.
2. How many litres is that per person per day, if the population of London is approximately 340 000?
Suppose that a brick was placed in every toilet tank in the city of London. What percent decrease would there be in the amount of water being treated on the average per day? [Assume that the brick displaces one litre of water and that the typical person flushes a toilet four times per day.]

Jake Lopers

Jake Lopers is Account Manager with the Port Perry, ON, branch of the Canadian Imperial Bank of Commerce.

Jake, what is a mortgage?

A mortgage is a loan that you use to buy a house.

How do you determine how much money a person can borrow when buying a house?

One of the factors we consider is a person’s income. We like to ensure that household expenses do not exceed 32% of gross income. We also like to make sure that the total of household expenses and other loan costs do not exceed 40% of gross income.

So if I have a car loan I may not be able to get as big a mortgage.

Yes, possibly. If your car loan payments take 5% of your gross income then it would not make a difference. However, if your car loan payments are 15% of your income then your household expenses should not exceed 25% of your income.

What are household expenses?

These expenses include mortgage payments, property taxes, and heating costs. And if you are buying a condominium, we include half your condo fees.

What do you mean by gross income?

Gross income is the amount of money you earn before any deductions, such as income tax or pension contributions.

What other factors affect how big a mortgage can be, Jake?

Mortgage interest rates play a big role. The higher the interest rate the more it costs to carry a mortgage.

Could you give us an example?

If your mortgage is $100 000 and the interest rate is 6%, your monthly payment over a 25-year amortization will be $640. On the other hand, if the interest rate is 9%, your monthly payment will be $828.

What do you mean by amortization, Jake?

The amortization period is the length of time you will take to pay back the mortgage. Most mortgages have an amortization period of 25 years. Some people choose to pay back the mortgage sooner, in 20 or 15 years, which means that their monthly payments will be greater. For example, a mortgage of $100 000 at 8% interest would cost $764/month if amortized over 25 years but would cost $949/month if amortized over 15 years.

Do you save a lot of interest costs if you pay off a mortgage in a shorter amortization period?

Certainly. A mortgage of $100 000 at 8% interest, amortized over 15 years instead of 25 years would save you $58 380 in interest payments.

How much of a down payment would I need to buy a house?

A 25% percent down payment would likely qualify you for what’s called a conventional mortgage. You can buy a home with as little as 5% down. However, if you have less that 25% to put down, you must apply for a high ratio mortgage. This means that your mortgage will need to be insured, which adds to the cost of your mortgage.

How does your credit rating affect a mortgage?

The credit rating or credit worthiness of a person is determined by their history of paying bills and making loan payments. A poor credit rating will reduce the amount of money you can borrow for a mortgage.

Something to Think About

What is a mortgage?
What are household expenses?
What factors affect how much a person can borrow for a mortgage? Explain.
What is meant by amortization period?
What is a high ratio mortgage?

Marg Franklin

Marg Franklin works for Barclays Global Investors, the world’s largest institutional investment management company. Marg’s job is to take technical, complex investment information and communicate it in a meaningful way to clients, prospects and the general marketplace.

Marg, how do you use mathematical modelling in your work?

The type of investing that we do is referred to as quantitative investing. That is, we look at all kinds of data and find relationships and meaning in that data that we can exploit. We use mathematical modelling to quantify and implement those relationships.

Could you give us an example?

One of the things we look at in our models is value. We are always seeking stocks that are priced cheaply relative to their fair value. To determine if a stock is under- or over-priced, we have developed a model that takes information from a company’s financial statements and manipulates it in ways that help us understand whether the stock is a bargain or too expensive.

What variables do you include in your models?

If I tell you I’d have to kill you … just kidding. The models we use are confidential. However, some typical variables that investment models take into account are a company’s assets, liabilities, its growth rate, as well as the price to earnings ratio of its stock.

How do you ensure your models will work?

The first thing we do is ensure that our models are sensible, intuitive, consistent and additive. What comes out of the model is only as good as its underlying fundamental principles, so we must be sure that what we’ve captured in our model makes sense. One can always find results in data that may be consistent or additive but not sensible or economically intuitive.

Could you give us an example, Marg?

A great example of this is the correlation between women’s skirt hemlines and the direction of the US stock market – when hemlines are up, so is the market. This seems to hold true from a statistical perspective, because we have seen it across time. However, it doesn’t make financial sense and so we would not include this in our model.

What makes a model consistent and additive?

If a model is consistent, then it works across a variety of timeframes. And anything we incorporate in the model must be additive, that is, it must contribute to the power and robustness of the results. Otherwise, it’s not worthwhile to include and clutters your model. We spend considerable time testing all of our models, using in-sample and out-of-sample data.

Could you explain these terms?

In-sample data is data used while you are building the model. Out-of-sample data is data that has not been touched while you were building the model. The beauty of out-of-sample data is that it allows you to run the model as if you were in real-time because you have not manipulated the model in any way to conform to this data.

What do you think of math, Marg?

I think in any aspect of work and life these days it’s critical. Much of what I work with is the capture of human emotion – fear and greed – in a quantifiable or mathematical way.

Something to Think About

1. How does Marg use mathematical modelling?

2. What does it mean when a model is:

a) sensible or intuitive?

b) consistent?

c) additive?

3. What is:

a) in-sample data?

b) out-of-sample data?

Jane Howe

Jane Howe is an exploration geologist from Vancouver, British Columbia. Jane explores around the world for various minerals such as: gold, silver, copper, lead, zinc and cobalt.

Jane, tell us about your work.

My work takes me to remote areas around the world (Canada, Peru, Argentina, Chile). Usually when I go exploring, I stay in a small tent camp and I travel around by helicopter, float plane, boat or 4 wheel-drive truck (if there are roads). I have also used mules, horses, all-terrain vehicles, and bikes to get to where I have to work. A typical day of fieldwork involves wandering around in remote areas with topographic maps, looking at rocks. If I think the rock might contain the minerals I am interested in, then I use my rock hammer and bash the rock to pieces, take a sample (about one kilogram of rock) and send it to a laboratory for chemical analysis. After I have spent some time in the field mapping and sampling the rocks, I return to Vancouver to evaluate the geochemical results of all my rock samples, write a report and draw a geology map which shows all the rock types in the area.

What type of math do you use in your work?

Geologists use statistics to evaluate and analyze geochemical results to determine anomalous levels of elements in the rocks. This helps us decide whether to do further exploration. We use univariate statistics to evaluate one element at a time (i.e., gold) and multivariate statistics to compare many elements (i.e., gold, silver, copper) to see if there are any inter-relationships between the elements. In order to get around in the field while we are exploring, we use maps and a compass; this requires an understanding of map (x,y) coordinates and directional measurements. We use trigonometry to determine the location and distribution of rocks below the earth’s surface, and to help us draw maps in three-dimensional space. We use volumetrics to determine the volume of rock, gravel or other material in a particular area of a mine or quarry.

Do you use any mathematical models to help make predictions?

We use statistical models to determine anomalous levels of elements within a group of rock samples. Hydrogeologists use complex models, which incorporate rain, snow, evaporation, and drainage rates to determine rates of discharge and recharge within a watershed (to ensure sufficient drinking water is available for a community). Half-life or decay curves are frequently used by geochemists to determine how long it will take for uranium or other radioactive elements to become chemically inert. Palaeontologists also use these same decay curve models to age-date fossils. Geophysicists use models to define rock characteristics such as density which in turn helps seismologists triangulate measurements to determine where an earthquake occurred, and how intense the quake was on the Richter scale.

Jane, can you tell us more about half-life or decay curves?

For example, Uranium (²³⁵U) occurs in minor amounts in many different types of rocks. Uranium is an unstable element which over time “decays” to lead (²⁰⁶Pb). There are many steps along the way, and many different “daughter” elements are created as a by-product of the decay of Uranium. The actual rate of decay is measured as a “half-life” – the time it takes for half of the “parent” element to decay to the “daughter”.

How does the Richter scale work?

The Richter magnitude scale was developed in 1935 by Charles F. Richter as a mathematical device to compare the size of earthquakes. On the Richter Scale, magnitude is expressed in whole numbers and decimal fractions. For example, a magnitude 5.3 might be computed for a moderate earthquake, and a strong earthquake might be rated as magnitude 6.3. Because of the logarithmic basis of the scale, each whole number increase in magnitude represents a tenfold increase in the size of the earthquake.

What do you like about your job, Jane?

The best part about being an exploration geologist has to be the travel, the daily variation and physical and mental challenges. A major part of my work occurs outdoors and I love the fact that I don’t have to stare at the same four office walls all day long. The opportunity to see wildlife and scenery that very few other people will ever experience is very exhilarating. Sometimes I work in high-altitude, mountainous terrain and marvel at the speed and proficiency with which mountain goats can move along the slope and kick rocks down on my head. Other days I find myself hiking along the cold, wind-swept, rocky coastline of the Arctic Ocean watching belugas rub in the shallow water. Some days find me crossing a high, desert plateau in South America on the back of a mule. The days that I must spend stuck in the office can be such a bore!

What made you decide to become a geologist?

There was really no one thing that made me want to become a geologist, but my family always seemed to encourage an interest in the world around me. This interest was stimulated over many years, with family holiday trips to Tyrell Dinosaur Park (in Alberta), tours of mines (Sudbury and Goderich) and oil refineries (near Edmonton). My big sister always gave me lots of cool birthday and Christmas presents which usually involved books about crystals or animals or other neat science things. I enrolled in Chemistry at university, but after my first work term at a copper-lead-zinc mine in Timmins, I was hooked on mineral exploration and I switched to earth science immediately.

Is it true that we eat rocks, Jane?

Yes, salt is a rock (and no, pepper comes from a plant). Feldspar is a very common rock-forming mineral and is frequently crushed and used as a “thickener” in milkshakes, coffee creamer. Fertilizers which we use in our gardens are all made from crushed rocks (Potassium, nitrogen, and phosphorus). The water that you drink contains all kinds of minerals (fluoride, chlorine, sodium, etc.) A lot of people also rub rocks all over themselves: baby powder is made with talc, a type of crushed rock

Something to Think About

What does Jane like most about her job?
How does Jane use statistics?
How does Jane use trigonometry?
What does Jane mean by volumetrics?
How does Jane use coordinate geometry?
How do palaeontologists use half-life or decay rates?
How does the Richter scale work?

Blake Palmer

Blake Palmer is a real estate agent with Remax Centre City Realty in London, Ontario. He has been a real estate agent since 1979.

How does a real estate agent make money, Blake?

Real estate agents make a commission by selling property. Generally speaking, we make money only when a transaction is closed or completed. Typically, the seller pays the commission, which is usually 6% of the purchase price of the property.If there is another involved in the sale, that agent will be paid a portion of the commission, usually half of the 6%.

What type of expenses would you have?

As a salesperson, you can generally opt to work one of two ways. Under Option 1, you can choose to pay all your own expenses. Under Option 2, you can have the broker pay for those expenses. If you choose Option 1, all, or almost all of the commission is yours. If you choose Option 2, you will work on what is called a “split” with the broker you work for, keeping a percentage (usually 40% or 50%) of the money that you generate in commissions to cover the cost of their expenses plus a profit for them.

Which option do you prefer, Blake?

Option 1 is the best way to go if you are a good agent making a good living. If you’re going to be lousy at it, choose Option 2. I’m an Option 1 guy.

How much are your expenses?

Not including vehicle expenses, my monthly business-related expenses average around $1100-$1200 a month. Those expenses have to be paid whether I make sales (and money) or not.

Do you use math in selling real estate, Blake?

You absolutely need math. Percentages, for example, are a key part of any realtor’s life – obviously in figuring out my commission! Also, in establishing upper limits for financing for buyers, calculating monthly payments for people with respect to their mortgages and other housing related expenses. There are other areas of the business which require the use of math, like estimating closing costs for buyers and collecting and remitting 7% GST on my services.

When do you make the most sales?

Realtors tend to make more sales when the economy does well, and people have jobs so they can afford to buy. The business tends to be somewhat “seasonal” in that the spring (March, April and early May) tend to be the busiest times. The most popular closing days for transactions are around June 30^th, and most of these transactions are negotiated 60-90 days before that date. I find that I tend to generate 65-70% of my income in the first 6 months of the calendar year.

What makes an agent successful, Blake?

A good agent must be a good listener. You have to listen to people so that you know what is important to them in a house and then find it for them. You also need to be relatively patient and unflappable. No two situations are exactly alike in real estate and usually things do not go as you would expect them or like them to go. Being a good negotiator also helps.

What do you like most about being a real estate agent, Blake?

The best thing about being a real estate agent is being your own boss and being able to work (for the most part) when you would like to and take time off when you’d like to. It is also exciting to be involved in what is probably the biggest purchase or sale that most people will make in a lifetime.

Something to Think About

How do real estate agents use math?
How does a real estate agent make money?
If Blake, along with another agent, sold a house for $176 000, how much commission would Blake make under Option 1? Under Option 2?

Doug Metcalf

Doug Metcalf has worked in the construction industry since 1970 and at the Lake Scugog Lumber Truss Plant, in Port Perry, since 1978.

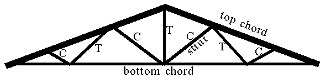
Doug, what exactly is a roof truss?

It’s a structure used to support a roof. A typical roof truss is the one shown on the right. On the outside it has two rafter components called the top chords and a ceiling component called the bottom chord. Within a truss there is configuration of struts, called a web. The web is usually arranged in a triangular pattern that gives a truss its strength. The truss is held together by toothed metal connector plates that are pressed into the joints.

Where are trusses made?

We make trusses in our plant. The cutting, assembly in jigs, and pressing of connector plates is done with machinery developed especially for this industry. We fabricate trusses for residential, farm and commercial buildings.

Would you be able to make a truss without using triangles?

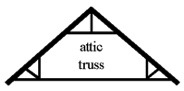
The web configuration used to construct a truss can vary, but usually forms a number of triangles within the perimeter shape of the truss. The struts that make up the triangles support the truss by performing alternating roles of compression (C) and tension (T), as shown in the diagram. It is possible to build trusses that do not have a web configuration, such as the attic truss (see diagram below). Attic trusses have an open area to allow for living or storage space. These trusses have limitations of span and load support due to their lack of total triangulation.

What variables do you consider when you design a truss?

The architectural features of a building dictate the main description of a truss, such as the span, or length, and the slope of the top chord. Regardless of the truss shape, it must be designed to withstand the climatic conditions at a particular geographic location, such as snow and wind loads. Also, we have to design for varied dead loads that could be imposed from things such as large air conditioners positioned on commercial roofs. The simplest truss to design would be one that has a symmetrical, triangular shape and is uniformly loaded. Once we have identified the basic outside shape or profile of the truss and the load it must support, the variables we have to work with are truss spacing, lumber size, species and grade, and web configuration.

Once you define these variables, how do you go about designing a truss?

We use a computer program to analyze the ability of a truss to support a particular load. The initial description of the truss to be analyzed by the computer is based on our judgement and experience. Subsequent fine tuning of the truss design is done by observing the original analysis results and then altering lumber sizes, grades, etc. to create the most economical truss that will do the job required of it.

How do you decide what a truss costs?

Truss cost is the result of the truss design and is comprised of lumber, connector plate cost, and labour. The biggest challenge is designing the unusual truss shapes for some of the radical building designs that we see.

Doug, what do you like best about your job?

With the variety of trusses we build, our work is always interesting.

Something to Think About

What is a truss?
What is a web?
What variables does Doug take into account when designing a truss?
What role do triangles play in the design of a truss?
What role does geographic location play in the design of a truss?
Trusses are often used in railway bridges. Where else would you find the web design used in trusses?

Whitney Cohoon

Whitney Cohoon is a farmer on the outskirts of Port Perry, ON. Her family farms about 900 acres of land.

Were you always a farmer, Whitney?

I started out in medicine. I was a research assistant when I first met my husband Bill. When we moved to Port Perry we started with a horse, then some sheep, then pigs, and now cattle and chickens. And we have some donkeys too.

What type of farming do you do?

Mostly we raise cattle and chickens.

How does a farmer make money, Whitney?

When it comes to cattle, we buy young steers and heifers when they are about 700 to 800 pounds and we raise them for four to five months until they are about 1200 pounds. We try to buy young stockers, which is another name for young steers and heifers, when their price is low and hope that the price is higher when we sell them.

What does it cost to buy a young stocker?

At the moment the price is about 95 cents per pound. But the price varies.

So you make money on the weight that the cattle gains?

Exactly. But remember that there are other costs involved. For example, we have to feed the cattle hay and corn, and we also give them antibiotics when they first arrive to make sure they are healthy.

What do the expenses add up to?

We grow our own hay and corn. But typically, a bushel of corn costs about 55 cents, and a stocker will eat about a bushel a day – a little less at first while its body gets used to the grain and up to two bushels a day when it reaches full feed. And you have to pay for the farm and the buildings, fences and farming equipment.

But you do make a profit.

Usually, yes.

How many stockers would you raise per year?

About 150 to 200.

What other animals do you raise?

We raise chickens as well. We grow about 16 000 chickens five times a year.

How long does it take to raise a chicken?

About six weeks.

How do you make money raising chickens?

We buy poulets at about 52 cents each and cockerels at about 60 cents each. These are tiny chicks, by the way. We sell them when they reach a weight of about 1.7 kilograms. The selling price at the moment is $1.16 per kilogram.

What are your expenses?

For each set of 16 000 chickens, we spend about $2 660 on starter feed for the first three weeks, then about $4 400 on grower feed for two weeks, and about $4 670 on finisher feed during the last week. Heating costs probably average at $1 000 per crop. Then there are electricity costs, straw for bedding, and maintenance of the barn. And we typically lose 2-5% of the poulets.

What do you like about farming, Whitney?

I like the routine of walking the barn to check on the chickens. I like feeding the cattle and watching them grow. This takes 1-2 hours every morning. I also like the field work – planting crops in the spring and harvesting them in the fall. Sometimes it’s very hard work, about 16-18 hours per day. But I wouldn’t trade it for city life. I enjoy getting up every morning and working on the farm.

Something to Think About

What does Whitney like about farming?
How much weight, in total, do Whitney’s cattle gain in one year? Her chickens?

Tom Ferrio

Tom Ferrio is vice-president of Texas Instruments’ Educational Solutions business. He helps develop calculator products for use in schools and provides support for teachers.

Who uses calculators, Tom?

Almost everyone uses calculators, but they use them for very different things. Most families have one or two simple calculators that can add, subtract, multiply, and divide for doing calculations around the home. Students are now the largest group of calculator users. Students use many calculators with scientific functions and even more advanced large screen graphing calculators that are very useful in high school and college math and science. Professional engineers and scientists all use calculators but tend to purchase them less frequently than students.

How do engineers and scientists use calculators?

Engineers and scientists today all have computers to use in their work. But calculators can’t be beat for doing straightforward calculations like evaluating a formula. The computer excels at more complicated work that may need a large spreadsheet, sophisticated statistical computation program, or a specialized design program.

Calculators can do a lot of the math we once learned in school. Do we still need to learn the math if the calculator can do it for us?

We definitely still need to learn math, but this changes which topics should be emphasized. Complete mastery of pencil-and-paper arithmetic can be de-emphasized to allow time to study richer problem-solving topics. Before the invention of calculators, it was very important to know how to do long and complicated calculations by hand, that was the only tool available. As a result, a large part of the mathematics learned in school was the step-by-step manipulation of numbers to do things like addition, subtraction, multiplication, division, square roots, logarithms, and more advanced functions. However, today’s technology has made pencil-and-paper arithmetic largely obsolete. Today’s high-powered technology allows students to quickly move beyond basic arithmetic skills and learn real mathematics.

What do you mean by real mathematics, Tom?

Workers in jobs seldom use pencil-and-paper arithmetic. In today’s world, more sophisticated mathematics skills are needed:

the ability to use mathematics to solve problems where the formula isn’t given
knowing what computations need to be done with data and when the data is adequate and accurate enough to get meaningful results
mental math – the ability to do simple computations accurately without pencil and paper, which still requires basic arithmetic skills, and the ability to mentally compute an estimate for more complex arithmetic problems
using calculators and computers in problem solving – companies expect workers to know how to use modern technology tools.

How does a calculator think? For example, when I enter 2 + 2, how does the calculator get the answer 4?

A calculator is really just a very small computer, actually with about the power of a 1970’s computer but shrunk down into a very small package. Inside the calculator is a computer chip and a memory chip that contains some built-in software. The software is just a series of instructions that look for keys to be pressed and then take action based on the key. When someone presses 2+2 on the calculator the software is just storing it away in memory. Then when the person presses = the software sees that it needs to add the two numbers and uses some complicates steps to compute 4 and then display it.

Something to Think About

Who uses calculators?
Why does Tom think that paper-and-pencil arithmetic is less important today?
Do you agree with Tom? Explain.
Do you think that a calculator ‘thinks’?

Amanda Stuart

Amanda Stuart is a Corporate Account Coordinator for Campbell Bros. Movers. She arranges moves for employees of McDonalds, GM Diesel, Union Gas & Union Energy, and the University of Western Ontario, to name a few. Amanda lives in London, Ontario. She has a seven-year-old daughter, and two lively cats.

What exactly do you do in your job, Amanda?

My job is to coordinate the moving of household possessions world-wide. I have moved people around the block, within Ontario, across Canada, and even as far as Hong Kong, Saudi Arabia and Australia. I calculate the cost for the move, set up for special services, and ensure that all customs procedures are properly followed.

Do you move things other than regular household items?

I also arrange for the safe transportation of vehicles and pets. I have personally arranged the relocation of laboratory and testing equipment for a team of researchers to Alaska, cages for monkeys, and priceless rocking chairs for a group of museums.

How do you use math in your job, Amanda?

I use math in almost every aspect of my job. All moves are based on either weight or time taken to complete the move. I often convert pounds into cubic feet to price storage and overseas shipments. I also develop tariffs for a company, which outlines in detail the level of discount for each service provided, such as, packing, appliance service, and transportation of the household goods.

Do you use mathematical formulas?

The tariffs I just mentioned are really formulas for calculating the cost of various services. Also, to price a household weight of, say, 10 000 lbs for storage, I would need to use a formula to estimate the number of cubic feet. This is actually a very simple formula as I would just divide by 7. It turns out that 10 000 lbs is about 1428.6 cubic feet The formulas are basic, and used by almost every moving company.

Do you price local moves differently than long distance moves?

A local move (within a 35-mile radius) is calculated based on the number of movers and the number of hours required. An average move within a city is based on 1 hour for every room of furniture. A 3-bedroom home, moving on a “month-end” time would be priced as follows: 6 rooms + 1 hour for travel = 7 hours $92.00/hour 7% tax = $689.08. For any local move that is 7 rooms or more, 3 movers are required at $122/hr. A long-distance move is generally based on weight miles.

What factors affect the cost of a move?

Prices change due to fluctuation in gas prices (for long distance moves). Also, certain days of the month are considered “peak” time, and for a local move increase the amount per hour that you spend. Cost is also affected by whether we do the packing or not.

What do you like about your job, Amanda?

My job is wonderful! I have the opportunity to meet people from all over the world! I am very lucky to have found a job that I enjoy so much. It is forever changing, which makes it exciting, and yet is the same because everyone has “stuff” that they call their own, and everyone wants to be sure that when they move, whether it be around the block, or around the world, they need to feel that it will arrive safe and sound. It is my job to make sure that it does.

Something to Think About

What type of math formulas does Amanda use in her job?
What would be the cost of a local move for a family living in an eight-room house?
What factors would affect the cost of a long-distance move?

MENU

Mathematicians

Professionals using math at work

Gilbert Labelle

Nathalie Sinclair

Karen Amanda Yeats

Walter Whiteley

Carolyn Kieran

Chris Essex

Ved Madan

Larry Davidson

Jake Lopers

Marg Franklin

Jane Howe

Blake Palmer

Doug Metcalf

Whitney Cohoon

Tom Ferrio

Amanda Stuart