(c) 2021 George Gadanidis
Infinity in your heart

For millennia, infinity has been a source of wonder and awe. It has captured our imagination. It has confused us, entertained us and surprised us.
We live our lives in finite spaces. Can infinity exist in our world?
Although infinity is big, our minds and our hearts are bigger. And, as you will soon discover, we can even hold infinity even in the palm of our hand!
MUSIC VIDEO
To inspire you, we have tried to capture the wonder and awe of infinity in a music video.
The above song, written by George Gadanidis and performed by Ian Parliament, Ryan Casselman and Alex Gadanidis, is a parody of Moonshadow by Cat Stevens. Animation by Jessica Taylor Charland.
WORKSHOP MENU
| MENU | TOPICS COVERED |
| A. Infinity in your hand B. Infinity in a walk C. Mathematician interview D. Infinity performances E. With code | — area representations of fractions — infinity & limit — how mathematicians think — history of mathematics — artistic/story representations — coding extensions |
A. Infinity in your hand
A.1. INFINITY IN YOUR HAND

Is it possible to hold infinity in the palm of your hand, as William Blake suggests in his poem?
“To see a World in a Grain of Sand And a Heaven in a Wild Flower, Hold Infinity in the palm of your hand And Eternity in an hour.” William Blake, Auguries of Innocence
What do you think?
A.2. SHADING INFINITE FRACTIONS
Let’s shade squares to represent an infinite number of fractions.
For example, the image below shows how to represent the fraction 1/2.

And the image below shows how to represent the fraction 1/4.

Now you do this, using identical squares, like the ones shown below.
- Sketch these squares on a piece of paper
- Or, print this PDF handout of the squares
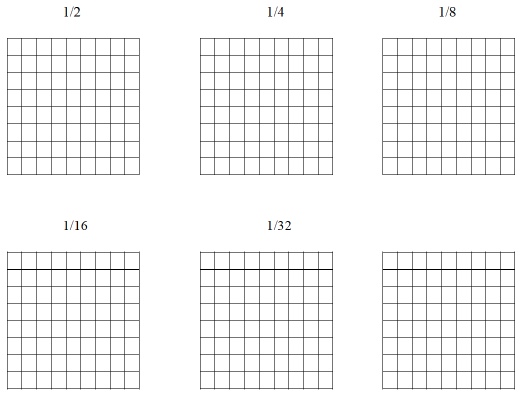

- Shade the first square to represent the fraction 1/2
- Shade the second square to represent half of 1/2, or 1/4
- Repeat for fractions 1/8, 1/16 and 1/32

Now you need a pair of scissors.
- Use the scissors to cut out the shaded parts (as shown on the right)
- Then join all the shaded parts to form a new shape
- Imagine doing this forever, shading, cutting out, joining
- How big would the new shape be?
- Would it fit in your room? In your house? In your town or city?
A.3. At the AI Academy
At the AI Academy, robots learn to think mathematically by doing the same activity as above.
A.4. Wonder

The activity above was designed to help you experience the wonder of holding infinity in your hand!
Anthropologist Ellen Dissanayake (author of Homo Aestheticus: where art comes from and why) says that humans naturally enjoy experiencing, creating and sharing wonders.
What do you think? It this true for you?
A.5. STORYTELLING

Brian Boyd, distinguished professor of literature at the University of Aukland (author of On the origin of stories: evolution, cognition, and fiction) says that humans are storytellers.
He adds that creating a good story involves solving the artistic puzzle of offering surprise, insight and a sense of wonder.
Is the infinite fractions activity a good math story to share? Does it offer mathematical surprise, insight and a sense of wonder?
A.6. AT THE MOVIES

The writer and filmmaker Jon Boorstin (author of The Hollywood eye: what makes movies work) explains that movies offer us the pleasure of surprise, where we can flex our imagination and see the world in new light.
When we watch a movie, we typically guess ahead. Boorstin explains that audiences pay for movies not to have their predictions confirmed, “but moment to moment they want to be wrong […] to be surprised” (p. 50).
Is this true for you? Do you prefer predictable movie plots or do you like to be surprised?
A.7. SHARE A MATH STORY

Share what you learned about infinity and fractions in a square with a friend or family member.
Share in a way so they experience math surprise and insight.
Ask them:
- What did you learn?
- What did you feel?
- What else do you want to know?
What did you learn from this sharing experience?
B. Infinity in a walk
B.1. WALKING OUT THE DOOR

Here’s a puzzle: It is possible to walk out an open door?
Imagine walking to an open door in this way:
- Walk half way to the door
- Then, walk half of the remaining distance to the door
- Then, walk half of the remaining distance to the door
- Keep doing this forever
- Will you ever get to the door?
- Will you ever walk past the door?
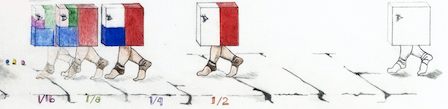
Stuck? Try it another way:
- Don’t think about the fractions
- Just walk to the door
- Then stop and look back
- Yse your imagination to see the infinite number of fractions you walked to get to the door
B.2. INFINITY IN HISTORY

The ancient Greek philosopher Zeno (495-430 BC) maintained that it was impossible for someone to walk to the end of a path because to do so they would have to travel an infinite number of distances:
- Half of the path distance (1/2 of the path)
- Half of the remaining 1/2 path distance (1/4 of the path)
- Half of the remaining 1/4 path distance (1/8 of the path)
- and so on …
This creates a paradox:
- On the one hand, we know that we can walk to the end of the path, and even beyond
- On the other hand, when we think of the infinite number of fractions we walk through, we are confused
B.3. HARE & TORTOISE

Here is one more of Zeno’s paradoxes:
If a hare gives a tortoise a head start in a race, the hare will never be able to catch the tortoise.
Think of it this way:
- By the time the hare reaches where the tortoise started, the tortoise will move a little farther
- By the time the hare reaches to where the tortoise moved to, the tortoise will move a little farther
- By the time the hare catches up to where the tortoise moved to, the tortoise will move a little farther
- And so on …
Such infinity paradoxes puzzled mathematicians and philosophers of the past.
B.4. SHARE A MATH STORY
Share what you learned about infinity and walking to the door with a friend or family member.
Share in a way so they experience math surprise and insight.
Ask them:
- What did you learn?
- What did you feel?
- What else do you want to know?
What did you learn from this sharing experience?
C. Mathematician interview

We interviewed mathematician Graham Denham (Western University) and he completed, extended and discussed some of the infinity activities above.
C.1. FRACTIONS 1/2, 1/4, 1/8 …
- How can we represent the fractions 1/2, 1/4, 1/8, 1/16, 1/32 and 1/64 as shaded areas?
- How do they relate to one another?
- What if we extend the pattern?
C.2. FRACTIONS IN A SQUARE
- “How much of a square will the fractions 1/2, 1/4, 1/8, 1/16, 1/32 and 1/64 fill?”
- “It would nice to visualize these in the same place. Let’s stuff all of these fractions in the same box. In how many ways can I actually do this?”
C.3. 1/2 + 1/4 + 1/8 + … = 1
- How can the sum of a never-ending sequence of fractions have a finite sum?
- 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64
= 63/64
= 1 – 1/64 - “It looks like there’s some suspicious pattern going on here.”
- “It turns out that you can make some real mathematical sense out of saying that an infinite sum is actually equal to 1.”
C.4. GEOMETRIC SERIES
- 1/2 = 1 – 1/2 = 1/2
1/2 + 1/4 = 1 – 1/4 = 3/4
1/2 + 1/4 + 1/8 = 1 – 1/8 = 7/8 - “You can get as close to 1 as you want. So mathematically we’d say that this represents a limit that converges to the number 1. It converges from below.”
- “It’s a famous problem. It’s called a geometric series.”
C.5. 1/3 + 1/9 + 1/27 + … = 1/2
- “We can do the same game with one-third.”
- 1/3 + 1/9 + 1/27 + 1/81 + … = 1/2
- “I like that picture a lot because as I look into it I see this fairly important basic mathematical truth inside the picture.”
c.6. TWO SERIES IN A SQUARE
- 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + …
= (1/2 + 1/8 + 1/32 + …) + (1/4 + 1/16 + 1/64 + …)
= 2/3 + 1/3
= 1 - “That’s kind of fun. I suppose then if you tried to re-arrange these in other ways you could probably also find other patterns and see some other ways in which the infinite sum fits in the box.”
At the AI Academy: Two series in a square
C.7. INFINITY ACROSS THE GRADES
- “I see that some kids have been doing this in the classroom … someone even dissected the square into triangular regions … that’s very beautiful as well … it’s nice to have a project where you can feel free to play and put things together in more than one possible way.”
- “In university level mathematics it’s not so far off. This particular topic is pretty interesting because … this process of taking a limit … is one of the core ideas in Calculus.”
C.8. 0.9999… = 1?
- “I have to confess something that bothered me when I was in about grade 5.”
- “How is it possible that 0.99999… = 1?”
Such infinity paradoxes puzzled mathematicians and philosophers of the past.
C.9. SHARE A MATH STORY
Share what you learned from the interview with Graham Denham with a friend or family member.
Share in a way so they experience math surprise and insight.
Ask them:
- What did you learn?
- What did you feel?
- What else do you want to know?
What did you learn from this sharing experience?
D. Infinity performances
D.1. in grade 2
Grade 2 students in Brazil engaged with similar investigations of fractions and infinity, and prepared the song below, called “Infinito”, which they performed for their school community.
D.2. In Grade 3
In Ontario, Canada, grade 3 students wrote skits of how they might share their learning at home. The skits were turned into lyrics for a song, which was performed by Indigenous recording artist Tracy Bone and Bob Hallett of Great Big Sea at a math concert.
D.3. In A PAINTING
The painting below, hanging in the main hall of St. Matthew the Evangelist Catholic School, in Whitby, Ontario, shows the math/infinity art created by students.

D.4. At the AI Academy
Three bots investigate infinity + art.
D.5. in a summary of ideas
D.6. CREATE A MATH PERFORMANCE
Create a math performance about infinity, such as:
- a poem
- a song
- math art
- a short story
D.7. SHARE
Share your performance with a friend or family member.
Ask them:
- What did you learn?
- What did you feel?
- What else do you want to know?
What did you learn from this sharing experience?
E. With code
E.1. MODELLING INFINITY WITH CODE
Follow this link to investigate infinity + limit by editing snippets of code: https://colab.research.google.com/drive/1D7Z7Uxsw-qgwG5odFxzWZ6oDbL3SH4u7?usp=sharing

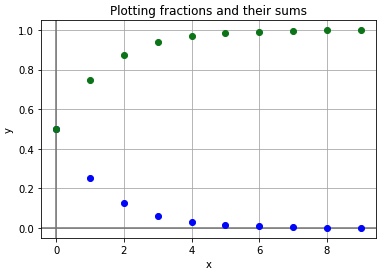
E.2. MODEL OTHER FRACTION PATTERNS
Edit the code to model the sums of each of these series:
- 1/4 + 1/16 + 1/64 + …
- 1/2 + 1/8 + 1/32 + …
- 9/10 + 9/100 + 9/1000 + …
Investigate series of other fraction patterns.
E.3. SHARE
Share what you learned about infinity and coding with a friend or family member.
Share in a way so they experience math surprise and insight.
Ask them:
- What did you learn?
- What did you feel?
- What else do you want to know?
What did you learn from this sharing experience?